小信号模型、跨导
数学中我们有一个经典的思想:微分思想。
设函数y=f(x)在x0及其附近有定义,如果函数值f(x)在点x0处的改变量Δf(x0)可以表示成自变量改变量的一次项a(x0)Δx与自变量改变量的高阶无穷小量o(Δx)之和,即
Δf(x0)=a(x0)Δx+o(Δx),则称函数f(x)在x0处可微,a(x0)Δx称为f(x)在x0处的微分,记作df(x0)=a(x0)Δx。
在小信号分析中,我们利用这个特点去求交流变化量产生的电流影响。求完之后,再加上输入的直流偏置信号,就可以得到实际的电流值。
举个例子,比如输入的栅源信号是Vgs+VGS,分析小信号时,只看Vgs,这样在电路中其作用产生的Ids为IDS关于VGS(直流信号)求偏导后乘以Vgs,这里的IDS关于VGS求偏导就定义为跨导gm。对于一个mos,常见的跨导有三类:gm、gds、gmb。
三种小信号模型
根据数学式子的一步步推导,我们可以得到IDS的电流为
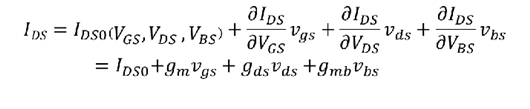
如果只看交流信号有
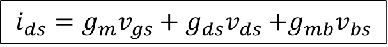
1.只考虑栅源电压
该形式只考虑栅源电压对电路各处的影响。
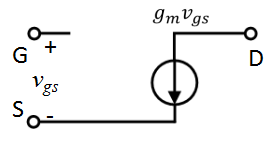
2.在01基础上考虑沟道长度调制效应
有两种形式,因为两端电压Vds的不变性,可以等效为一个阻抗。
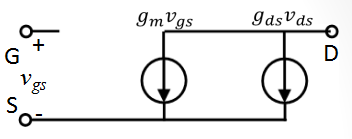
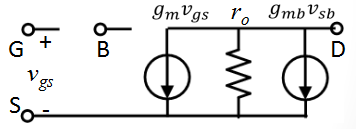
3.在02的基础上再考虑体效应
〈烜芯微/XXW〉专业制造二极管,三极管,MOS管,桥堆等,20年,工厂直销省20%,上万家电路电器生产企业选用,专业的工程师帮您稳定好每一批产品,如果您有遇到什么需要帮助解决的,可以直接联系下方的联系号码或加QQ/微信,由我们的销售经理给您精准的报价以及产品介绍
联系号码:18923864027(同微信)
QQ:709211280


